视频终于上传成功了!原来是格式的问题,视频中的音频必须是 44.1 kHz 采样、双声道格式才行。
从我马克到写完答案、上传视频的一天里,本问题下已经涌现了许多好答案,这才是知乎该有的样子!
一、预备知识
人的耳朵和大脑在处理声音信号时,根据信号中特定特征反复出现频率的高低,有两种明显不同的模式。当特征反复出现的频率较低时,人可以分辨出它每一次出现的时刻,把信号理解成节拍;但当它反复出现的频率很高时,打拍子就跟不上了,此时耳朵就发挥了作用,把这个信号理解成乐音。这里面低频和高频的分界线,在 20 Hz ~ 40 Hz 左右。
人的耳朵与大脑的上述特点,跟信号处理中的「短时傅里叶分析」非常相似。短时傅里叶分析,是把一段长信号截成许多帧,对每一帧进行傅里叶变换求得频谱,再把各帧的频谱并排起来得到整段长信号的语谱图。语谱图的横轴是时间,纵轴是频率,颜色表示能量的高低。短时傅里叶分析的一个重要参数是帧长(也叫窗长)。当信号中特定特征出现的频率较低,低于帧长的倒数时,它就会在有些帧中出现,在有些帧中不出现,于是在语谱图上形成沿横轴重复的图样。当特征出现的频率较高,比帧长的倒数还高出一截时,它就会在所有帧中都出现(甚至出现多次),于是这种特征的频谱就会在时间轴上铺展开来,在语谱图上形成沿纵轴重复的图样。
利用短时傅里叶分析,可以把人的听觉感受转换成视觉来呈现,有助于理解。下面的视频,就播放了一系列频率不同的脉冲串,同时画出了波形和语谱图。脉冲串的频率由 1 Hz 开始,逐渐加倍,直到 512 Hz。信号的采样率是 16384 Hz,根据奈奎斯特采样定理,语谱图的频率上限就是 8192 Hz。做短时傅里叶分析时使用的窗长是 512 个采样点,即大约 31.3 毫秒,其倒数为 32 Hz,大约就是节拍和乐音的分界线。可以看到,当脉冲串的频率超过 32 Hz 后,语谱图上的纵纹就开始转变为横纹,同时你听到的东西也从节拍转变成乐音了。
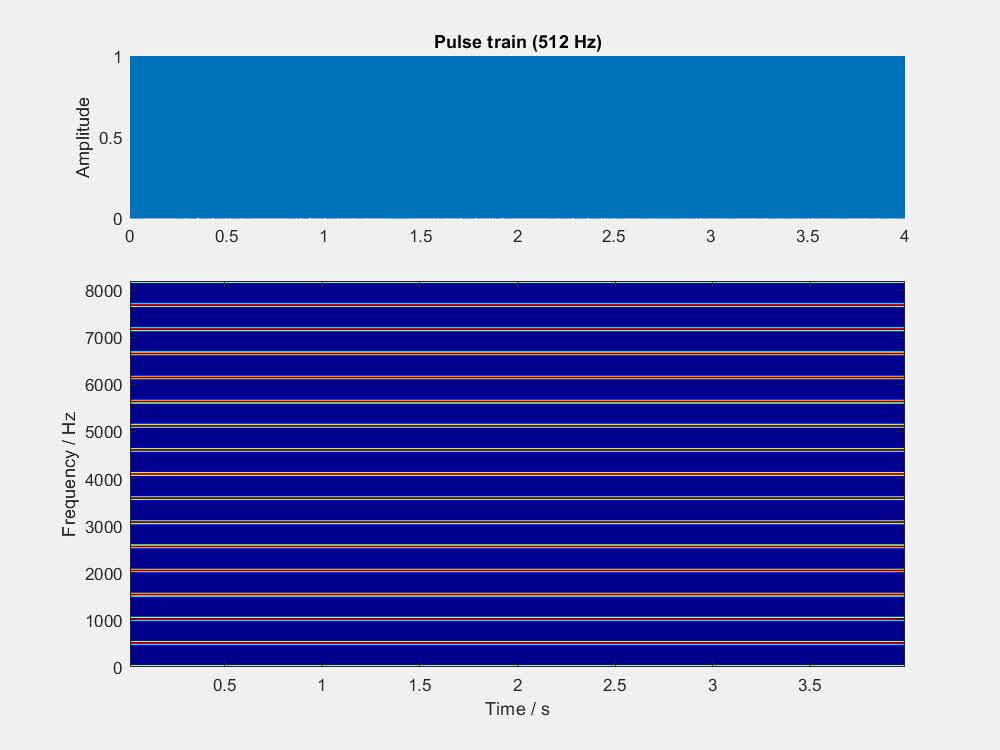
看过上面的视频,你应该能体会到短时傅里叶分析的时域分辨率是有限的:当脉冲在时间轴上靠得太近的时候,它们在语谱图的时间轴上就分不清了,反倒会沿频率轴形成图样。其实,短时傅里叶分析的频域分辨率同样是有限的,这是因为「截取一帧」的操作相当于把信号与窗函数相乘,这会让频谱产生弥散。如果信号中有两个频率分量的频率太过接近,它们在语谱图的频率轴上也会分不清,而是沿时间轴形成图样,这就是下面要分析的「拍频」现象。
二、两个正弦信号的叠加
我们从最简单的情形开始:先假设两个乐音都是最简单的正弦波。设它们的频率分别为 f+\Delta f 、 f - \Delta f 。为简单起见,设两个正弦波的幅度相等、初相均为 0。则两个正弦波之和可以表示为:
x(t) = \sin[2\pi (f+\Delta f) t] + \sin[2\pi (f-\Delta f) t] \qquad (1) \\
根据和差化积公式,上式也可以写成:
x(t) = 2 \sin( 2\pi \cdot f \cdot t) \cos (2\pi \cdot \Delta f \cdot t) \qquad (2) \\
两个式子是等价的,但根据 \Delta f 的大小不同,其中有一个式子会比另一个式子更直观地描述语谱图及人的听觉。
当 \Delta f 很小时,(1) 式中两个频率分量的频率就很接近,于是在听觉上就都分不开了。而根据 (2) 式,信号可以看成是一个频率为 f 的振动 \sin(2\pi \cdot f \cdot t) ,但是它的振幅按 |2 \cos (2 \pi \cdot \Delta f \cdot t)| 在变化。这个振幅的变化频率 2\Delta f 很低,于是就能被听成节拍,这就是「拍频」现象。此时 (2) 式能更直观地描述听觉。
当 \Delta f 较大时,若按 (2) 式理解,则振幅的变化频率 2\Delta f 较高,无法被听成节拍,故 (2) 式并不直观。相反,(1) 式中两个频率分量的频率相差较大,可以被分开,于是人就会把信号听成双音。此时 (1) 式能更直观地描述听觉。
下面的视频,展示了 f = 440\text{ Hz} , \Delta f 由 1 Hz 逐步倍增至 256 Hz 时,两个正弦波叠加的波形和语谱图。可以听到,当 \Delta f 达到 32 Hz 时,听觉上虽然还略有抖动,但其实已经很像双音了;语谱图上两个频率分量也快要分开了,沿横轴变化的图样也基本消失。
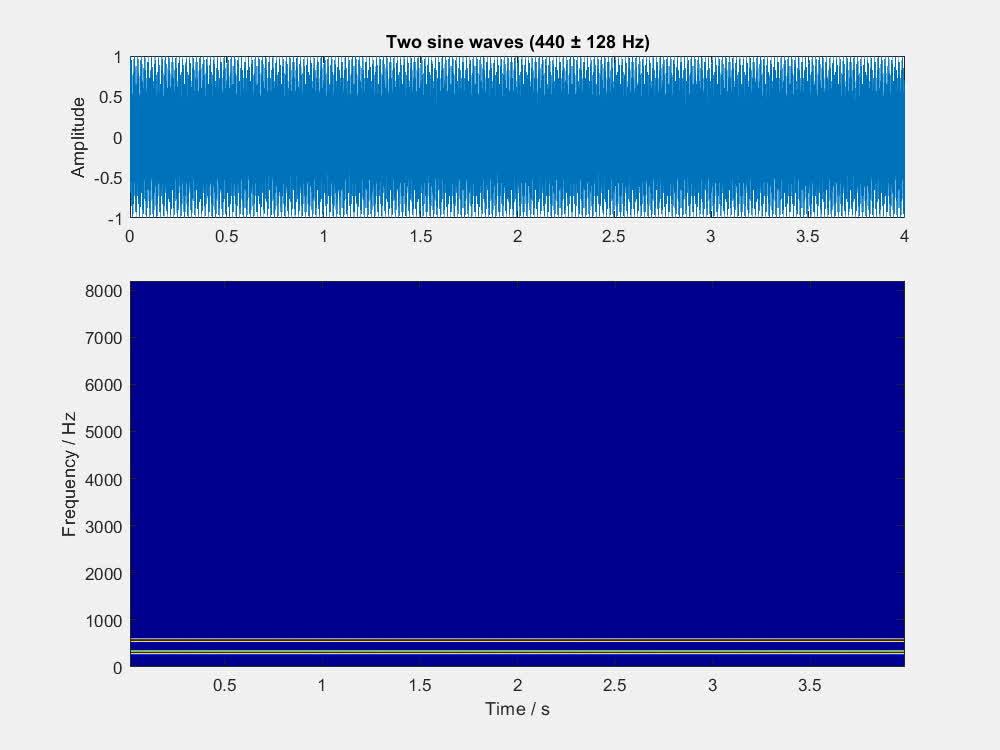
如果题主用 440 Hz 和 493.8 Hz 两个正弦波叠加,就相当于 f = 466.9\text{ Hz} , \Delta f = 26.9\text{ Hz} 。这跟上面视频中 \Delta f = 32\text{ Hz} 的情形比较接近,处于拍频和双音的临界,如果仔细听,还是能听出一点儿拍频的。
上面的分析中为简单起见,设定了两个正弦波的幅度相等、初相均为 0。实际上,初相对问题的分析没有影响;幅度不相等时,振幅没有彻底减小为 0 的瞬间,因此拍频现象会弱一些,但没有本质不同。
三、两个非简谐信号的叠加
大部分乐器产生的声音都不是单纯的正弦波,而是具有许多频率分量的非简谐波。在这一节中,我用方波来举例。同样设两个方波的频率为 f+\Delta f 、 f - \Delta f ,幅度相等,初相均为 0。两个方波的叠加可以表示为:
x(t) = \text{sign}\{\sin[2\pi (f+\Delta f) t]\} + \text{sign}\{\sin[2\pi (f-\Delta f) t]\} \qquad (3) \\
其中 sign(正数) = 1,sign(负数) = -1,sign(0) = 0。
方波的叠加就没有和差化积公式了,所以我就不多做计算,直接上视频了。下面的视频展示了 f = 440\text{ Hz} , \Delta f 由 1 Hz 逐步倍增至 256 Hz 时,两个方波叠加的波形和语谱图。
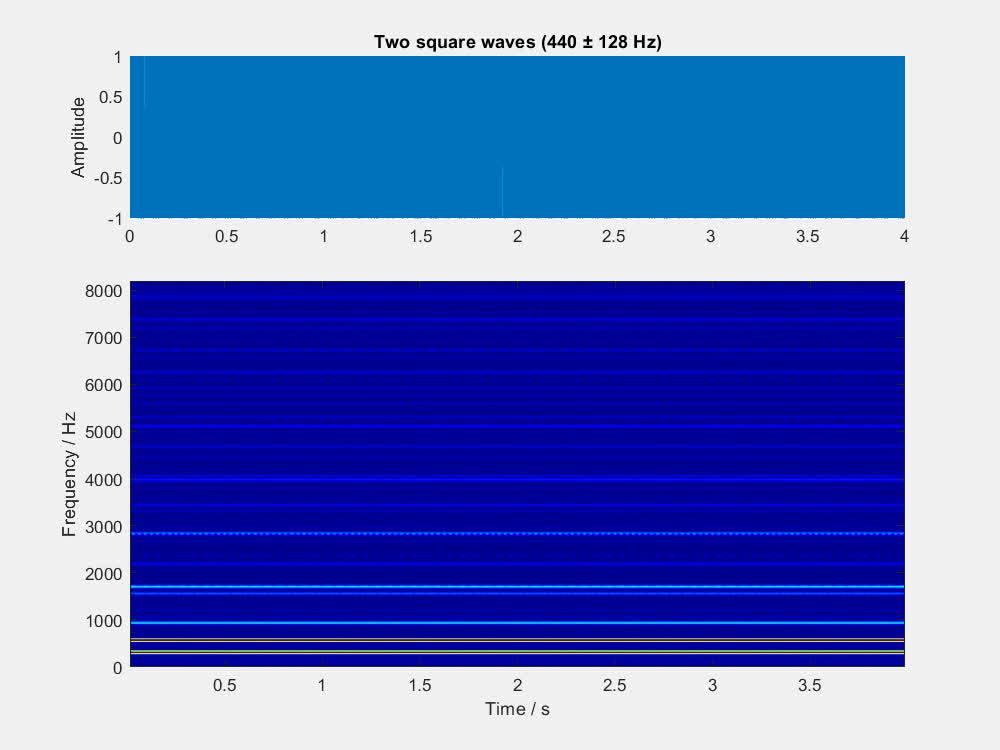
可以听到,哪怕 \Delta f 只有 4 Hz 的时候,拍频现象就已经不太明显了。从语谱图上可以看出,虽然方波的基波和三次谐波(方波没有偶数次谐波)形成了沿横轴变化的图样,但更高次的谐波都已经能在频率轴上分开了。这些高次谐波在一定程度上淹没了基波和三次谐波的拍频现象。
题主在钢琴上弹奏 440 Hz 与 493.8 Hz 这两个音,听不出拍频,应该就是由于高次谐波的淹没作用。
有心的读者也许注意到了,当 \Delta f 较高时,有些比较高频的分量会形成拍频。比如当 \Delta f = 32\text{ Hz} 时,在略高于 6 kHz 处有谐波形成了拍频。这个拍频,其实是 (440 - 32) Hz 的 15 次谐波 6120 Hz 与 (440 + 32) Hz 的 13 次谐波 6136 Hz 叠加形成的。不过,由于方波 n 次谐波的幅度只有基波的 1/n,上面这个拍频的能量极弱,是听不出来的。
四、三个正弦信号的叠加
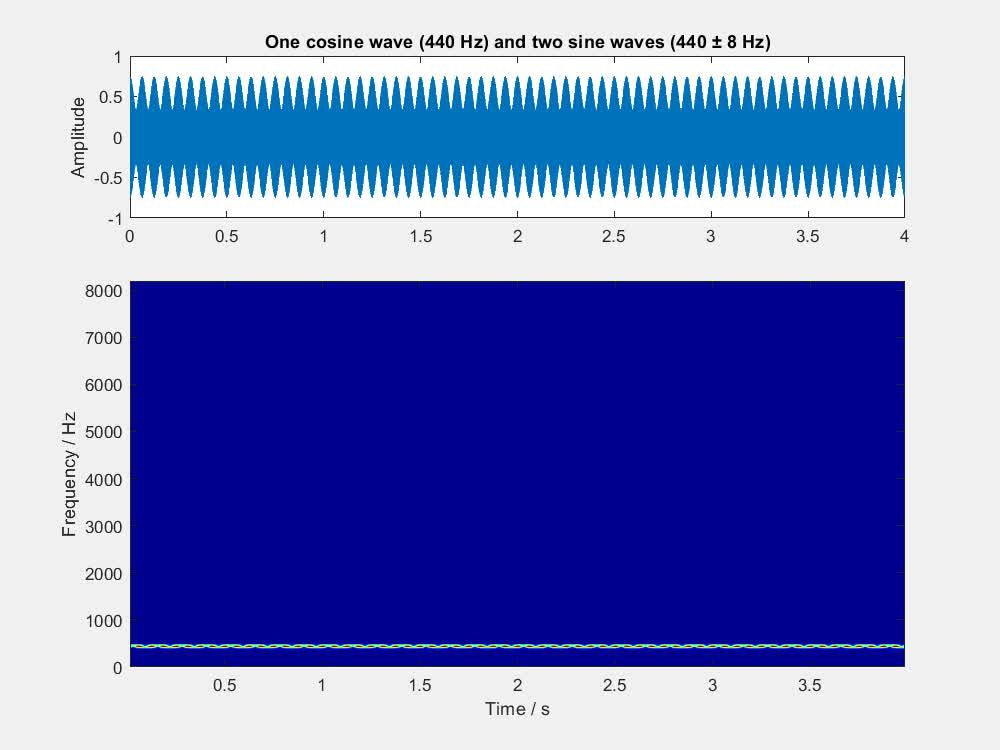
设三个正弦信号的频率分别为 f 、 f + \Delta f 、 f - \Delta f ,幅度相等,初相均为 0。它们叠加后的效果如下面的视频所示。三个正弦信号叠加产生的拍频现象比较复杂,其包络呈现大包小包相间的模式。由于小包的阻隔,拍频转化为三音的临界频率比两个正弦信号叠加时高了一点儿:当 \Delta f = 32\text{ Hz} 时,听觉感受还是以拍频为主;但当 \Delta f 达到 64 Hz 时,听觉感受就以三音为主了。
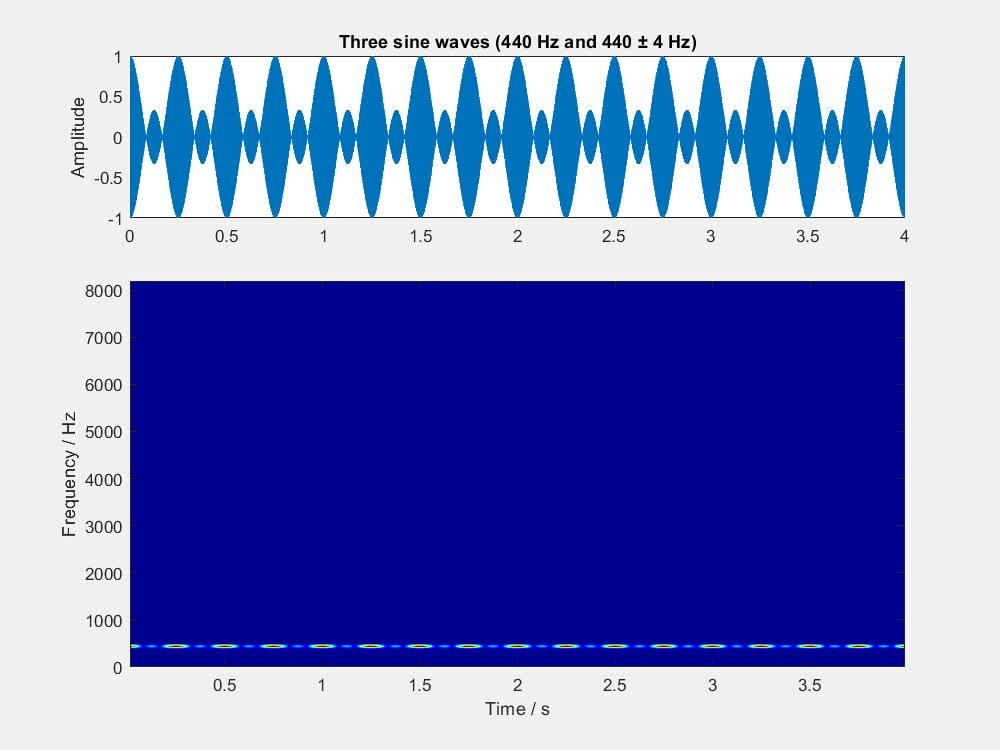
三个正弦信号叠加时,信号之间的相位关系也会有影响。比如,若把频率为 f 的那个信号由正弦改为余弦,则叠加效果如下所示。此时并没有大小包的交替,但音高呈现出了渐高、渐低交替的模式(可以叫「抖音」?);这种模式在 \Delta f = 16\text{ Hz} 时尤为明显。当 \Delta f 达到 32 Hz 时,抖音开始转变为三音,到 64 Hz 时听起来就完全是三音了。
五、总结
两个正弦波叠加时,如果频率差在一定阈值以内(粗略地说,差 50 Hz 以内吧),就能听出拍频现象。
如果是两个非简谐波叠加,那么基波形成的拍频会受到不形成拍频的高次谐波的淹没,上述阈值会降低不少。
如果是多个正弦波叠加,那么根据它们之间相位关系的不同,上述阈值可能会略有调整,也可能形成「抖音」等比拍频更复杂的现象。

